Why Heavier Things Don’t Fall Faster
Galileo is not just one of the Italian-sounding words found in the lyrics of “Bohemian Rhapsody”.1 Galileo is, of course, the name of the famous Renaissance-era Italian scientist who is most famous for inventing the telescope. He also discovered what is probably the most shocking, counterintuitive, flat-out bizarre little property of physics that most people ever come across. I’ve attempted to explain lots of bizarre physics theories to my friends and family, from quantum mechanics to relativity, but no physics concept I’ve explained has met with more outright disbelief and arguments than this one. The concept? Simply, that heavier things don’t fall faster than light ones. If you take a golf ball and a bowling ball and drop them off the side of a building, they’ll both hit the ground at the same time.
For many of you out there, this little factoid might not be surprise — as unusual science facts go, this one is pretty well-known in popular culture by now. It turns out that as long as air resistance isn’t a major problem, EEVERYthing on planet Earth not already on the floor will fall at the same speed, if dropped from the same height. Things that are really really light, such as feathers, pieces of paper, my scientific credentials — these things get hung up in the air and DO fall slower than heavier things. But anything big enough that air resistance doesn’t matter (basically anything bigger than a golf ball) will fall exactly at the same rate.2
While most people hold the misconception that heavier things fall faster than light things, this misconception used to be considered an official honest-to-goodness law of physics, codified by Aristotle in ancient Greece. Only Galileo, however, decided to test it out. In what was probably one of the first buddings of modern science, Galileo did an experiment to test a law of physics, and found it to be completely wrong. Even though anyone could try it for themselves, no one actually bothered to try it, and even now people who could easily prove it to themselves simply deny that this could be possible. It’s still a point of discussion in my family to this day, a good decade after I first brought it up.3 Don’t believe it? Give it a try for yourself, then!
So what’s the deal? Why do we instinctively believe that heavier things should fall faster, and why don’t they? Well, the simple answer is a word describing an effect you’ve experienced if you’ve ever tried to move a sleeper sofa. If you ever agree to help your friends move, and you decide to tackle the couch, make sure to ask your friend if it has one of those fold-away beds in it. If you don’t ask, and it is a sleeper sofa, you’ll emit one of those embarrassing squeaks as you start to lift the couch and realize its much much heavier than you thought. Heavier things are harder to move — they have inertia. Ever watch those World’s Strongest Man contests on ESPN4? There’s always one event where they have to pull a Cessna with a rope. It takes a little while to get heavy things to move — a lot of force is required to get them moving at any speed. Likewise, when they finally get the Cessna rolling, it takes a lot of effort to stop it, or else it will keep on rolling off the tropical Pacific island they usually hold those contests on.
So what happens, when you drop a baby-grand piano off the roof, is that the force of gravity has to get that piano moving, and has to overcome the inertia of the heavy piano to get it moving. So while the piano is heavier than a golf ball, and so the force of gravity is greater on the piano than the golf ball, inertia is a lot harder to overcome with the piano. The greater force of gravity on the piano exactly balances the greater problem of inertia, and you wind up with the piano and golf ball moving at exactly the same speed. As a result, absolutely everything that falls will fall at the same rate — strictly speaking, everything falls with the same acceleration, about 10 meters per second squared.
So… why is this so counterintuitive? Why do we believe that heavier things should fall faster? Well, without delving into the psychology, I think the reason has to do with a special property of gravity, compared to all the other kinds of forces that we experience day-to-day. A giant blond Norwegian pulling on a Cessna with a rope is exerting a force. The engine of the Cessna is exerting another force to keep the plane up in the air (though hopefully not when a Norwegian is pulling on it). The guy sitting in the back row talking on his cellphone (despite being warned) will get a force applied to him when the stewardess slaps him with a rolled-up barf bag. Whenever a force is applied to an object, the object will start moving according to Newton’s Law:
If you know the force, and know the mass, you can figure out the acceleration. For example, if you know how strong the Norwegian can pull (the force), and know how much the plane weighs (the mass), you can figure out how the plane will move — it will start to accelerate, according to the formula above. If you’ve taken a physics class, you’ve done this sort of thing all the time.
That expression above works for any force, no matter what. But the force of gravity happens to have its own mathematical expression, which was worked out by Newton. Here’s what the force of gravity looks like:
where M is the mass of your object (golf ball, piano, or Norwegian), Mearth is the mass of the earth, R is the distance between the object and the center of the earth, and G is a constant number. If you got the value of all these numbers, you can plug them into this equation and figure out the force of gravity on the object — even if the object is out in space, like a satellite. It also applies to the force between the Earth and the sun that keeps us in the solar system.
So let’s follow the ol’ physics 101 routine, and use F = ma to figure out the motion of an object under the influence of gravity. For any force, you can use F = ma to find the acceleration of the object, if you know the force F. Well, we know the force, it’s the force of gravity. So let’s plug in the equation for gravity into F = ma:
Check it out — the mass of the object, which we’re calling M, is on both sides of the equation. Recall your 10th grade algebra class, that this means you can cancel M from both sides — it just drops out completely. You’re left with this expression for acceleration:
G is a constant, and the Mearth (the mass of the earth) doesn’t change. Everything on the surface of the earth is pretty much the same distance from the center of the earth, so R doesn’t change very much (unless you scrape up enough funding to get into orbit, Lance Bass). So for all practical purposes, the acceleration is the same for everything on earth!4 For everything in everyday life, a, the acceleration you get from gravity, is fixed. That’s why everything on earth, no matter how light or heavy, falls to the ground at the same time when dropped from the same height.
Isn’t it strange that mass gets to be in both formulas, in both F = ma (which is a universal law about how things move when any force is applied to them) and in the expression for gravity (which applies to just gravity, and gravity alone). Mass is the biggest double-threat since Bo Jackson. (Don’t remember him? Okay, Deion Sanders. You don’t remember him either? Shut up, kid. I know I’m old.) It’s a fundamental property of the force of gravity, and it’s instrumental in how objects start to move once a force starts acting on them. How come it gets to play both roles? The first people to think about this even discriminated between the two roles that mass plays, by calling the mass involved in gravity the “gravitational mass”, and mass involved in motion the “inertial mass”. The big mystery is why the gravitational mass is the same as the inertial mass. They didn’t have to be. This isn’t true for other forces, like electromagnetism — in general, forces depend on lots of things, but only gravity depends on mass.
The force that the Norwegian can use in pulling the plane depends on how strong he is, how well he’s trained, whether he’s keeping his shoulders down (or whatever the right technique is, I’m not too familiar with the best way to yank a plane on a rope). The electrical force between two charged particles depends on how big the charges are, and their sign (positive or negative). The force applied by a jet of water from a firehose depends on how much water is coming out and how fast its moving, which depends on the water pressure. The force a sailboat feels from the wind depends mainly on how much surface area the sails have, and how well the captain of the boat can angle the sails across the wind. For any force, you can figure out what the strength of the force depends on.
There are all kinds of forces out there in the world, but only a few are “fundamental” — all other forces can be boiled down to one of the fundamental forces. Gravity is one. Electromagnetism is another, and is the fundamental force behind most of the everyday forces you know and love — the reason you can push on a wall without falling through, for example, is that the electrons in your body are repelling the electrons in the wall from the electromagnetic force between them. There are only four fundamental forces, with the other two being the strong force, which keeps atomic nuclei together, and the weak force, which has a hand in radioactive decay. Every fundamental force has some quantity that is analogous to “mass” in gravity. For electromagnetism, it’s the familiar electrical “charge”. As we all know, like charges repel, and big fat charges repel each other a lot. For yer typical electron, the electron’s mass is what matters for gravity, and the charge is what matters for electromagnetism.
Just as we broke down gravity into an equation above, we can do the same for electromagnetism. Here’s what the electric force between two charges looks like:
where Q1 is the charge of the first guy, Q2 is the charge on the second guy, R is the distance between them, and 4pe0 is a big mess of constant numbers (just like G, for gravity). It’s got the same kind of structure, with charge Q playing the same role as mass M did for gravity.
All the fundamental forces have some quantity like this that plays the same role as gravity does for mass, (though it doesn’t always have the same mathematical formula). The strong force, for example, has a property the scientists call “color”. It doesn’t mean a real true color, but it’s just a term the scientists use — only quarks have “color”, and they’re way to small to have a real color to them. All of these forces involve some property of matter like “mass” or “charge”, and the property tells you how strong the force will be. Gravity acts strongly on something with a lot of mass, and electromagnetism acts strongly on something with a lot of charge. The analogy across all forces is so ingrained that you sometimes hear people refer to “color” as the “color charge”, and mass as the “gravitational charge”. The fourth fundamental force is called the weak force, and it’s analogous property is called “flavor” (which has nothing to do with taste, but is just a whimsical name physicists use to keep from naming yet another physics discovery after Einstein). So all fundamental forces have an associated property of matter that tells you how strong that force will act — for gravity, the strength of the force depends on the mass, and for electromagnetism, it depends on the charge.
So we come to the million-dollar question — how come the “charge” for gravity gets to also hang out in the universal law F = ma, which applies to all forces and matter? Isn’t this a conflict of interest? It’s as though a football quarterback gets to be one of the referees in his own game. The “Gravitational mass” is really the “charge” for the force of gravity, while the “Inertial Mass” is an essential part of Newton’s laws of motion. Why do they happen to be the same thing? They didn’t have to be. This little fact has been known for a while, but it wasn’t until Einstein5 that anyone really thought hard about how special this is. For gravity, and only gravity, the force depends on mass. Mass, by virtue of popping up in the equation F = ma, is intimately involved in the motion of all objects — it determines how fast the object will accelerate when you apply a force (any force) to it. Einstein thought long and hard about this, and thinking about this wound up leading him down the path to General Relativity.
Einstein’s solution to why gravity gets to double-dip was to assert that gravity is not a force! Mass is a member of the inertia team, and that’s all it does — gravity is not really a force, not like the other fundamental forces we discussed, and so mass is only involved in acceleration. (Technically speaking, some of the forces I’m talking about weren’t discovered yet when Einstein was thinking about this. Please don’t derail my train of thought by pointing this out.) His inspiration came from realizing that you can’t tell the difference between being accelerated through space and feeling the pull of gravity while standing still. Imagine flooring it while driving your 1995 Toyota Tercel — you feel pushed backward into your seat because you’re accelerating forward. It feels like a force pushing you back, but that’s an illusion — it’s really that the car is moving you forward. But imagine if you were blindfolded, and couldn’t tell the car was moving — you might for a moment feel as though you were standing still, and some force field was pushing you backward into the seat. Or better yet, imagine standing in an elevator, where the lack of windows means you can’t tell whether you’re moving or not. As the elevator starts to move, we all experience a little instant of feeling weightless (or of feeling really heavy, if the elevator is moving up). We of course know that the sensation is the elevator accelerating, but since we can’t see the motion directly, it feels like gravity just got dialed to a different setting for a brief moment. It would feel exactly the same to us if we were inside a completely stationary elevator, and someone outside were fiddling with the strength of Earth’s gravity.6
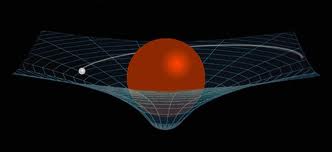
Essentially, Einstein said, if it quacks like a duck, it must be a duck — the force of gravity behaves suspiciously similar to an acceleration. The crucial clue is that “the same quality of a body manifests itself according to the circumstances as ‘inertia’ or as ‘weight’”, in his words.7 The unmasking of gravity as an acceleration, not a force, is the key concept in his General Theory of Relativity. I won’t get into it here in detail, mainly because I’m far too drunk. But perhaps you’ve heard simplified explanations of relativity describe gravity as a “warping of spacetime”. Einstein explained that gravity really isn’t a force after all, but it truly is an acceleration — when you stand still under the earth’s gravity, you’re really being accelerated8, by matter’s ability to warp space and time itself. And this warping is controlled by mass — the greater the mass of an object, the more it warps space-time around it. Imagine a bowling ball sitting on a trampoline — if you roll a marble across the trampoline it will wind up rolling down the slope to the bowling ball, attracted to it as though pulled by some force, but it’s simply following the “space-time” distortion caused by the ball. That analogy is wickedly oversimplifying, but captures the essence of the idea — gravity is not a force like other forces, that act directly between two objects. What we think of as gravity is really the feeling of being accelerated through space, the same feeling we get as our inertia resists being accelerated in our Tercel trying to outrace the cops.
I’m not even going to pretend I explained General Relativity very well, or even that explaining it does much to help my original point about light and heavy things falling at the same speed. But I find it fascinating that this odd little counterintuitive factoid led Einstein to completely overturn classical physics and win the race for Smartest Person Ever. But in the spirit of journalistic integrity, I feel an irresistible pull to return to why we feel that heavier things should fall faster than light things. I think we somehow intuitively understand that the strength of forces depends on how much “stuff” there is to feel the force, be it mass (for gravity) or size of sails (for wind force on a boat) to the size of the Norwegian (for the airplane pull in the World’s Strongest Man contest). We don’t intuitively recognize, however, that the “stuff” involved in the pull of gravity is the very same “stuff” involved in the inertia that resists getting things to move. And we definitely don’t intuitively grasp that gravity is not really a force at all, but instead a type of acceleration, harder to visualize but otherwise identical to the accelerations we feel in cars, elevators, and airplanes pulled by Norwegians.
So — that’s why heavier things don’t fall faster than light things. I realize that while perhaps entertaining, this article isn’t going to help whatsoever to convince you, if you are an unbeliever. It probably made it worse. If you insist that a bowling ball will hit the ground before a golf ball, and no egghead with a webpage will convince you otherwise, then we’ll just have to agree to disagree. But you can be sure of one thing — I’ve got the balls to prove it.9
Footnotes:
1. Funny that Galileo is also included in an Indigo Girls’ song. How cool of a scientist do you have to be to get a mention in multiple top-40 hits?
2. Those of you who know your physics will now be complaining, in a nasal voice, that I’m confusing velocity with acceleration when I say “rate”. Everything that falls will of course speed up as it falls, so strictly speaking, everything dropped will accelerate the same. The rate of falling increases constantly, but increases exactly the same way for all objects. I’m going do a lot of this vague blurring of technicalities to keep the article moving along, and I trust you agree that none of these will change the main point in any way.
3. An even more controversial topic at family functions is the fact that if you shoot a bullet from a gun perfectly horizontally, and simultaneously drop a bullet from the same height, they’ll both hit the ground at the same time. Of course the one you shoot will be half a mile away, but as long as the ground is flat it will hit the dirt at exactly the same moment as the bullet you simply let drop. My family demanded I prove it, using a potato gun, but the experiment was too much fun and I kept screwing it up.
4. Of course R isn’t exactly the same for everyone, but the difference in R between the top of Everest and the bottom of Death Valley is so small compared to the diameter of the earth that you’d never notice the difference in “a” without some expensive scientific equipment.
5. Einstein! Him again? You’re thinking “can’t I read a simple physics article without hearing about him again?” Despite his status as one of the most respected icons of humanity, as probably the smartest human in recent memory, he’s probably still underrated as a physicist. His influence is everywhere. It’s commonly recounted that he didn’t win the Nobel Prize for his development of the Theory of Relativity, instead for a supposedly obscure bit of work called the photoelectric effect. But you don’t often hear that he deserved it for the photoelectric effect — without going into details, it was this theory of Einstein’s that happened to be one of the very first quantum-mechanical theories. Essentially, in order to explain this “obscure” effect, he proposed that light came in discrete quantities, that we know call photons. So aside from creating Relativity, a completely new branch of physics, he was one of the founding fathers of Quantum Mechanics, the other completely new branch of physics invented in the 20th century. And if that weren’t enough, he explained a method for providing the first direct evidence of the existence of atoms (using Browninan Motion), developed the theory used for inventing lasers, first proposed superfluidity to be possible, and of course was the grandfather of the atomic bomb. Probably no other single person had more impact on the daily life of everyone currently living on this planet.
6. It’s no coincidence that fighter jets measure acceleration in “g”s, where one “g” is equal to earth’s gravity.
7. From his great book “Relativity: The Special and the General Theory”. This was his “popular exposition”, written for the common man to explain his greatest accomplishment. Great bathroom reading.
8. Don’t confuse the acceleration from gravity with the acceleration of the spinning earth, or of the earth hurtling through space as it orbits the sun. Even if you were perfectly stationary, and the Earth didn’t move or spin at all, you would be accelerating according to Einstein’s theory.
9. You didn’t really think I’d finish an essay like this without a joke about balls, did you? You obviously didn’t know me in junior high…





 Follow Timeblimp on Twitter
Follow Timeblimp on Twitter
… [Trackback]…
[…] Read More: timeblimp.com/?page_id=174 […]…
[…] than a golf ball) will fall exactly at the same rate.' I'm gonna go have some Ice Cream now… 'Why Heavier Things Don't Fall Faster' ~ Timeblimp.com —– __________________ ~ Think For Yourself ~ 10 January […]