A Cellular Automaton? In My Very Home?
Chances are, there’s a CELLULAR AUTOMATON somewhere in your house, right now. If not inside your house, there’s certainly one in your backyard. And up until recently, scientists didn’t even know this was possible. A rare few suspected it, but their warnings went ignored or ridiculed by the mainstream (including, I shamefully admit, me). Perhaps the only thing more deliberately, amateurishly misleading than the government’s stance on cellular automata is… this whole conceit for my introduction to this article. Wow. I’m really going with the old “This thing you’ve never heard of is in your home! Implied threat that it’s dangerous!” trope? This has to be the lamest way to prop up an article introduction in the history of this website. Boy, for your sake, I really hope this is going somewhere…
Alright, a cellular automaton is by no means dangerous, but it would be a little surprising to find one in your backyard. In fact, it would be a major discovery to find one in the natural world, anywhere. So what is it? It’s the name for a charming little quasi-game played by knowing nerds, and also for the whole field of research that has sprung up around them. The world of Cellular Automata is one of a handful of fascinating, mysterious, dare I say it sexy topics from science and math that are astoundingly cool but arguably not all that useful or applicable to the real world. (See also Complexity, Chaos theory, Emergent systems, Nonlinear dynamical systems, Fractals, Criticality, and of course Quantum Chaos.) Nobody doubts they’re cool — these fields are absolutely intoxicating. You probably have a book about one of them on your shelf right now, or perhaps a poster in your dorm room. But there haven’t been a whole lot of applications for them in the real world. Or, more importantly, demonstrations that living systems use them. Wouldn’t it be cool to learn that some organism has evolved a way to use chaotic systems to its advantage, somehow? That some complex system in nature uses some funky nonlinear effects to its advantage? It’s a tantalizing idea, but to date there are far more examples where living systems go out of their way to avoid these baroque nonlinear structures. A complex chaotic attractor might be interesting to us intellectually, but might be no different than plain old noise to an organism. The lack of nontrivial examples of some living system using them has led to somewhat of a cloud of cynicism over the whole enterprise — they don’t quite live up the hype, some say. And Cellular Automata (or “CA” for short) might be the most egregious example, as I’ll describe.

A “queen bee” — one of the many strange objects that emerge when you play with a cellular automaton. If you want to lose an entire day, check out more at Eric Weisstein’s Treasure Trove of the Game of Life (http://www.ericweisstein.com/encyclopedias/life/)
So what’s a Cellular Automaton? This is one of the more blatant examples of a name being way too intimidating for the concept it embodies — cellular automata are very simple, easy to make, not much more complicated than a game of Battleship. To understand a CA, first remember the rules of checkers. In checkers, your pieces hop around on a rectangular grid, and in certain circumstances a piece can make another piece disappear. Now, tweak the rules a little bit — say, give permission for checkers to reappear on the board, reanimated from the dead, in certain situations. Maybe, what the hell, make all the checkers just one color, instead of two opposing colors. And let’s tweak the rules for when checkers have to be taken off the board. Instead of disappearing when another piece jumps over it, maybe a checker has to go bye-bye if two other checkers wander up next to it. And that’s basically it – a “cellular automaton” is just a big checkerboard grid, with checker pieces appearing and disappearing over time, based on whatever rules you want to make up for each turn. People have experimented with all kinds of variations on the rules (e.g. when a particular checker piece has to disappear, how many colors there can be, 1D vs. 2D vs. larger-dimensional playing fields, etc.), and generally code them up on computers to watch the board evolve over time as a movie.
That’s it? Why the fancy name? Well, it turns out that if you pick your rules just right, all kinds of strange things happen on the board. Most of the time, nothing much special happens — maybe all the checkers die out, or maybe they multiply like rabbits and fill the entire board. The most common (and hence most boring) examples are where the CA reaches some bland “steady state” like these. Occasionally, though, you stumble across a set of rules for playing the game where the checkers create intricate patterns that propagate across the checkerboard like ripples on a pond. The patterns move around on the board, interact with each other, spawn new patterns — in effect, start to look like little life forms. By far the most famous of these is a rule set created by John Conway, called the “Game of Life” since it makes such startlingly lifelike creatures. Code this up on a computer, and you’ll see all these funny little shapes made from clusters of adjacent checkers, moving around the board and bumping into each other. A zoo’s worth of shapes have been discovered — they’ve been named “gliders”, “spaceships”, “boats”, based on their shape and behavior. There are even “guns”, persistent shapes that burp out gliders and other shapes. It’s frankly startling the menagerie of creatures that inhabit the Game of Life.
Lots of really smart people spend their free time exploring the world of cellular automata (CA), cooking up interesting examples, and generally out-nerding each other with what they can get their CA to do. Some CA’s can be used to solve problems, while others exhibit actual chaos (told you these areas are related). One person took it further, though — much further. Stephen Wolfram, the guy whom Wolfram Alpha is named for, and who invented Mathematica (the computer program that does your math homework for you), wrote a 74,142 page tome making the case that Cellular Automata should be considered a candidate for a unified theory of everything. It’s only a slight exaggeration to say that he basically said to forget about quantum mechanics, forget about string theory — Cellular Automata are the foundation of the universe. Or at the very least, are so important that they deserve to be the subject of an entirely new branch of science. At the time, I was just as enthralled by CA’s as everyone else, but skeptical of Wolfram’s claim that CA’s underlie much of what we see around us in the universe. Wolfram showed a ton of stuff you could do with CA’s, but showed very little evidence that anything in nature actually uses them. About the most compelling evidence he had to offer was how certain mollusc shells had patterns that kinda sorta resembled some of his CA’s.
Imagine my surprise when I came across this paper: “Evidence for Complex, Collective Dynamics and Emergent, Distributed Computation in Plants“, from David Peak, Jevin West, Sussanna Messinger, and Keith Mott. Whoa, that title has a trifecta of critical buzzwords: Complex? Emergent? Computation? Evidence??? These are all the right dog whistles to grab the attention of the seasoned nonlinear chaoplexologist. Is this finally an example of this stuff being used in a natural system? It’s sho ’nuff the closest I’ve ever seen. I’m admittedly not exactly Johnny-on-the-spot, since this paper came out in 2004. But still, I just had to devote an entire article to it, and to eat a little crow for doubting Wolfram. (Not much crow, but a little.)
I came across this paper while researching how plants secretly communicate with each other, which led to the question of whether plants are intelligent. The short answer? Don’t worry, keep eating your salad. Plants don’t appear to be conscious — they probably don’t have any sort of centralized intelligence capable of executive decisions, like us. They don’t have nervous systems, and no real way to transmit information rapidly from different parts of the plant (though see my other article on that very topic). But that doesn’t mean a plant can’t have some intelligence — it just has to develop ways to intelligently solve problems without such an internal communications system. For example, imagine your body aches all over (perhaps you’re hung over). Your brain will receive a “pain!” message from all around your body, and will integrate the information to decide what to do next (“skip the triathlon, go lie down”). But what if your brain only gets the “pain!” message from one single location? Say, your finger hurts because you’re absent-mindedly leaning on a hot stove. In that case it might take a completely different course of action. A plant doesn’t have this luxury — if something’s causing damage to one leaf, that leaf “knows” its injured, but the rest of the plant won’t know for a while — certainly not fast enough to do much about it.

Another strange pattern from Conway’s Game of Life. This has nothing to do with the paragraph it’s sitting in — I just like looking at these things.
So the plant as a whole needs to solve problems without any sort of fast-acting, central, decision-making brain. It behooves each part of the plant to act locally — that leaf could defend itself from a predator, for example, without having to rely on the rest of the plant. We humans don’t need this — our knee doesn’t have to defend itself from mosquitoes, because it can notify the brain to do something about it. But plants do — it would really be advantageous to plants to evolve some sort of distributed intelligence. Dare I say it, an emergent intelligence, something that arises from the collective whole of many simple, locally-interacting units.
Now, let’s talk about one of the biggest problems a plant faces, a problem we humans can’t really relate to — how easily a plant can dehydrate simply from breathing. A plant breathes through tiny pores in its leaves called stomata, through which it takes in CO2 from the air. But with stomata open, the plant loses water through evaporation. So the plant faces a tradeoff, having to judge how much to open its stomata given the ambient light conditions and humidity. On a global scale, the plant will walk the thin line by fully opening the stomata only when it feels very bright light (when it can really crank up the photosynthesis), and closing the stomata completely when in darkness. But a simple open/closed rule isn’t good enough — a plant could do even better by opening its pores just enough to optimize how much it can photosynthesize for a given amount of water loss. Plants continually tweak the proportion of stomata that are open to get the balance just right — for any transient fluctuation in sunlight or humidity, the plant’s leaf will respond by recalculating the optimal proportion of pores to open. Saying that the plant “calculates” might seem like a bit much, but the plant really is doing a calculation — it’s solving a problem given some stimulus, and making a decision. (In fact it’s a surprisingly sophisticated constrained optimization problem that you can solve with the calculus of variations. But you probably already knew that.)
Each leaf is on its own. Leaves have to be able to do this calculus problem themselves, and hopefully they collectively reach the right decision. Individual stomata can talk to each other, however — through some as-yet-unidentified mechanism, the stomata in a little local patch on a leaf can communicate and reach a consensus about how much to open. David Peak & company have a hunch that the way the stomata communicate together ensures that the plant as a whole will make the right call. If you design the stomata right, and constrain how they talk to each other just right, you can in principle rig it so that they’ll automatically tend toward the right answer to the CO2/water-loss tradeoff — you won’t need a central intelligence. How do they know this? Because Cellular Automaton researchers have been doing this for years. It turns out the stomata-opening question map to a well-known Cellular Automaton puzzle called the “density classification task“. It’s an example of asking a CA to solve a puzzle (or to perform a calculation), where the CA has nothing else but it’s own simple rules to guide it.
So what’s the density classification task? It’s quite simple, despite the grandiose name. (That whole grandiose name / simple concept thing keeps coming up.) Imagine a 2D cellular automaton where every little cell is in some random state, on or off. At the beginning the checkerboard grid looks like TV static. The challenge we issue to the CA is to tell us the most common state. One of the possible states will happen to be the most-common state, and we want to know which one. And we ask the CA to tell us the answer by gradually evolving until all cells in the grid have the same value. If at the end they all evolve to the correct answer, then the CA performed the computation correctly.
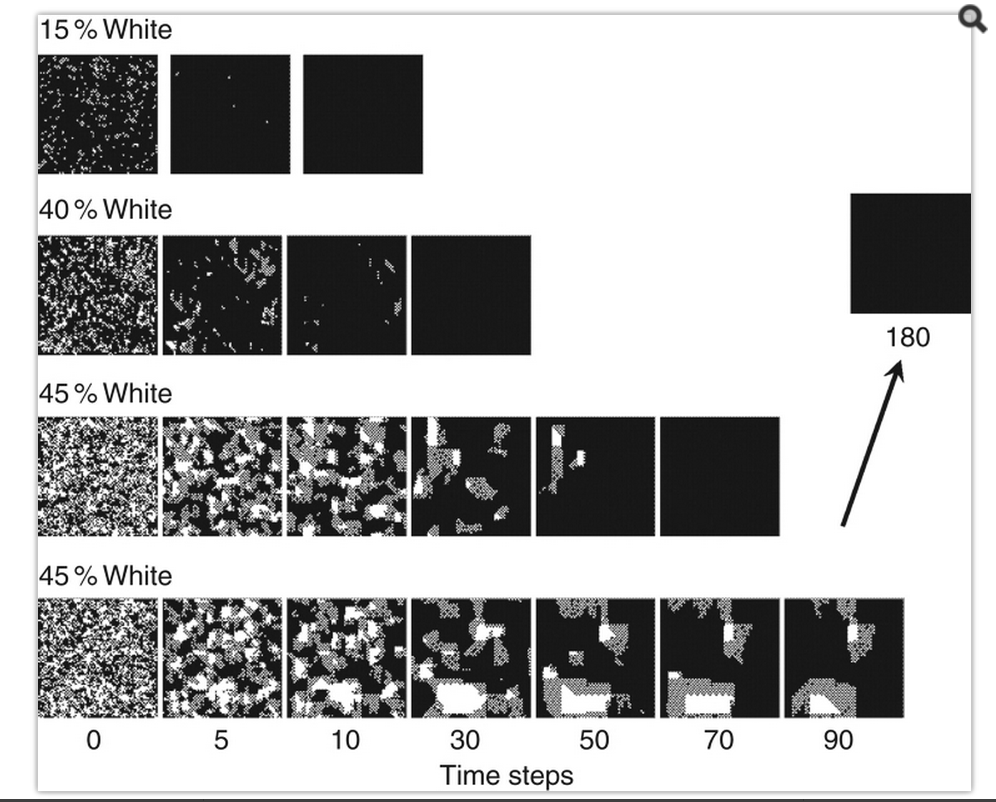
Sounds astoundingly easy, right? Finding the most common value (or “mode”, in statistical terms) is a breeze — just go through each cell and tally up the state in each, and count up all the votes. But remember, there’s no central intelligence in a CA — you’re not allowed to look at the state of all the cells. There is no “you”, no entity that is allowed to count votes — the cells have to act on their own, and they can only communicate with their neighbors. You let the CA evolve, as you do, and the cells work it out and eventually reach some final stable state. If that state is all uniform, and equals the right value, then that CA correctly performed the computation — it measured its own majority state, without needing any sort of agent or executive to count up across cells at the beginning. And there are CA’s that can do this. For example, Cellular Automaton Rule 184 can apparently solve it, albeit in one dimension. (“Rule 184” refers to a particular CA, using Steven Wolfram’s nomenclature. If you have an afternoon to kill, browse the hundreds of other CA’s at the Wolfram Atlas of Elementary Programs.) When I’m more ambitious I’ll build a nice movie showing a CA solving a 2D density classification problem, but until I do, here’s a graphic from the Park Crew, showing examples of CA’s solving the density-classification problem:
In the picture above, four different CA’s start out at some initial random state (on the left), gradually evolving over time by forming little patches of same-state cells (middle), and letting the neighboring patches battle it out with each other (going to the right). As the CA evolves, little domains of agreement form, where every cell in the domain agrees with the neighbors. Over time, the domains grow larger and larger (as a big domain convinces a disagreeing neighbor to flip), eventually taking over the entire space. At the end, everyone in the CA hopefully agrees on the same state, and that state is considered the CA’s attempt at answering the question. And it’s possible that a particular CA won’t get the right answer — if you choose the rules of interaction among the cells wrong, then the final state won’t be equal to the mode. Or even worse, it might not converge at all — it might never get out of the patchy state, failing to return an answer at all. Only certain specific CA’s will reliably provide an accurate answer. Even after you find yourself a nice accurate CA, some input states will be harder than others — notice in the figure above, the closer the initial black/white split is to 50%/50%, the longer it takes the CA to get to the right answer.
This might seem like a roundabout way to simply find the mode of a bunch of little cells, but remember that you have a severe constraint of only being able to work locally. The right answer has to emerge from the interaction of the cells over time. And why would we care about such a strange constraint? Surely, in any type of computer, you’re allowed to do something as straightforward as taking the mode… But the relevancy here isn’t for computers. It’s for systems that have just this sort of severe constraint — like plants! Park & the Parkettes hypothesize that the stomata on a plant leaf are using something pretty similar to a CA to get the CO2/water tradeoff solved. The research is still in the early stages, but they’ve collected evidence that whatever it is that the plant is doing, it looks awfully similar to a density-classification CA.
Park & his crew set up a nifty experiment where they were actually able to video the stomata-openness on a leaf, and how it changed over time. By immobilizing a leaf and subjecting it to stimuli (like strong sunlight, humidity changes, etc.), they can record the pattern of stomata openness across the surface of a leaf over time. And crucially, they can induce some sort of change in the environmental conditions, specifically to force the plant to solve the CO2/water tradeoff problem anew. Give the leaf a kick, and watch how it reacts. For this paper, they use a pretty simple stimulus — they simply make the humidity drop a little bit. The right answer is for the stomata to close, of course, but there’s a precise amount of closing that optimizes the CO2/water tradeoff. The little stomata on the leaves make their best measurement of conditions they can, and make a call. Most of the time, the problem is pretty easy — if humidity goes down, stomata should close. And this is what Park & co. see most of the time — all the stomata on the leaf dial their openness down a notch, to a lower value that is optimal for the new lower humidity. But occasionally the problem gets harder for the stomata to solve — they overshoot how much to close, for example. And neighboring patches on a leaf may come to opposite conclusions. In these cases, these little local patches battle it out, making their case for what the leaf as a whole should do. At first you see lots of variability among different parts of the leaf, but after a while they settle their differences and decide on a final value for stomata-openness. Here’s a video they took of the leaf surface, showing the little patches battling it out for supremacy:
At first, each stomata (stomatum?) makes their own decision about what to do, and many of them will be way off the mark — if you tallied votes at the start of the stimulus, you’d find a pretty random-looking pattern dispersed across the leaf surface. After a little time goes by, the stomata can communicate with their neighbors and form a consensus, making a little local patch who have all voted the same way. But any given little patch might still be voting wrong. A little more time goes by, and these little coalitions of stomata interact with each other, working out compromises and building larger patches of uniform voting. Eventually the patches grow so large that the entire leaf becomes a single voting block — the leaf has made a decision about how to respond to the stimulus. And if it uses the right rules for how stomata interact, it will come to the right decision. If the leaf could somehow poll everyone at the start, it could simply choose the majority vote and bypass all the infighting and dynamic patchiness. But there’s nobody there to take the vote, so the stomata are left to figure it out as a group. Presumably the plant has evolved just the rules of engagement of stomata to their neighbors to ensure that the evolution of the “voting” will come to the right conclusion.
The group hasn’t proved that the plants use cellular automata (or something akin to CA) to do the computation, but it sure smells like it. Their most convincing argument is statistical — and for this reason, I’ll be skipping it completely. Why? Because even I can’t make statistics interesting. (And I don’t understand these specific statistics anyway.) Suffice it to say that you can statistically measure certain characteristics of a 2D evolving system (be it a simulated Cellular Automaton, or a real living plant leaf), and it turns out that plant leaves quite resemble certain CA’s. It’s got to do with with Hurst’s rescaled range statistic, with the event waiting time distribution, and the power exponent of the spatial Fourier spectrum. Okay, I concede I won’t win a Pulitzer for investigative journalism by skipping these topics — but I’m really gunning for an Emmy anyway.
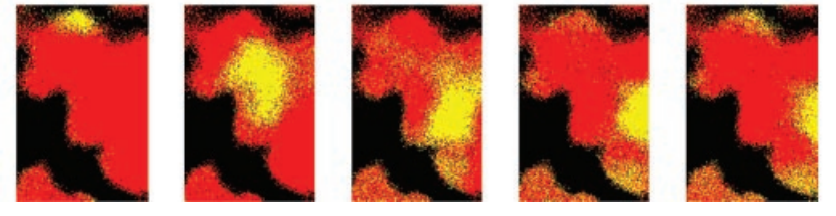
Perhaps a less-convincing but more evocative bit of evidence is the way these patches of “agreement” move about on the surface of the leaf. If you’ve ever explored Cellular Automata, you’ll know the real charm of them is watching the moving shapes and patterns that result. This is still circumstantial evidence, of course, but the moving blobs in the leaf stomata videos sure look similar to the evolution of cellular automata solving a density-classification task. The Halloween-colored image to the right shows a clip from Park’s leaf videos, where you can see a blob of closed stomatas in yellow moving down and to the right. Here’s a (somewhat large) video clip from the Park crew, showing better detail for these moving blobs:
mcl234_06_431_supp_video_file_2
It turns out that the “moving blob” phenomenon is important — in the world of cellular automata, rule sets that support such “moving patches” tend to be more accurate at the density-classification task. Some rules just don’t support coherent motion of little local blobs, and these rules tend to stall out and fail to converge on an answer. And having moving patches is also pretty convenient for a plant — remember, there’s no nervous system to transmit information across a leaf, so stomata on one side of a leaf have no way of communicating directly with stomata on the other side. Having the ability for little patches of agreement to move coherently across the leaf might be the only way for information relevant to the CO2/water-loss problem to be transmitted across the leaf.
Researchers have known for years about the patchiness of stomatal behavior on plant leaves, but the reason for it has always been a mystery. It’s conceivable that the plant could have simply evolved some way for individual stomata to be more accurate, not need any communication with neighbors, and so the leaf wouldn’t have any of this random patchiness — it could just uniformly adjust itself to the right answer. So why patchiness? Well, it’s possible there’s some constraint that makes accurate stomata hard to make, or it’s an evolutionary accident (“we chose inaccurate stomata, and we can’t turn back now”), but it might also be an intentional choice. Park and the crew contend that solving the problem this way, with lots of relatively dumb little units battling it out for agreement, might be more robust to noise and error a more conventional system.
Of course, there are some remaining questions:
- How do neighboring stomata talk to each other? Can we figure out the “rules” of how they talk, and see if they match up to the rules for Cellular Automata that can solve the same problem?
- Have we really proved yet that the stomata are a cellular automaton? No, not really — evidence is circumstantial right now, albeit it’s quantitative, statistical.
If you’re reaction to all of this is “pretty flimsy evidence that plants are actually doing Cellular Automatatation!”, then I grudgingly admit you’re right. And you need to work on your spelling of ‘Automaton’. But this is reflective of just how little evidence there is for the really interesting discoveries in Cellular Automata to be used by natural systems, rather than being some fascinating oddity. In the name of Wolfram, let’s hope there’s more to be found!
Further reading:
- Keith Mott’s Lab webpage, including the home of the stomatal patch videos
- A profile on this research in Nature




 Follow Timeblimp on Twitter
Follow Timeblimp on Twitter