Fun With Number Theory
Have you ever spent an afternoon perusing the dusty back alleys of recreational number theory? I mean, of course you have. We all have. There was that wild weekend in college, where I … well, I don’t actually remember what I did, but I do know they won’t let me use the Sieve of Eratosthenes anymore. Mathematicians have discovered some pretty wacky stuff in the far corners of number theory; let’s take a tour of some of our favorites…
Have you gotten the digits of pi memorized yet? Yes? Good. Then let’s recite the first thousand digits together. [Pauses, while you recite Pi] Excellent! Did you happen to notice what happened back there around digit 762? At the 762nd decimal place, Pi has a sequence of six 9’s in a row. Pretty freaking fantastic, eh? OK, maybe you’re not exactly floored, but that spot is famous, and even has a name – the Feynman Point. It’s named after the famous physicist Richard Feynman, who is the obvious choice if you’re going to name a segment of Pi’s decimal representation after someone. The presence of six 9’s in a row seems mildly unusual, until you work out the math of the likelihood of seeing such a pattern in a random string of digits — then it’s not so unusual. But still — you don’t have a piece of Pi named after you, do you?
The famous number of the beast, from the Book of Revelation in the Bible, happens to have some interesting numerical properties, including the fact that it’s the sum of the squares of the first seven prime numbers:
22 + 32 + 52 + 72 + 112 + 132 + 172 = 666
Spooky, eh? Sounds like a good basis for the plot of the next Nicholas Cage action thriller. More interesting factoids and nomenclature:
– the sum of all numbers on a roulette wheel is 666
– A number containing the digits of the beast number is called an apocalyptic number
– A number having 666 digits is called an apocalypse number. The Fibonacci number F3184 happens to be an apocalypse number, for example.
– A number where the first n digits of the fractional part of the number sum to 666 is called an evil number. And I’m sorry to report, Pi is evil — the first 144 digits of Pi sum to 666.
– Finally, the number (10666)! is called the Leviathan Number. And it’s huge — it’s got about 10668 digits, so it’s a number you couldn’t write out in longhand on a piece of paper that would fit into the known universe.
When was the last time you had a McNugget? Mmmm, little fried morsel of unidentified chicken protein. Back in my day, they came in orders of 6, 9, or 20 nuggets, though these days you can get 4 of ’em in a Happy Meal. A McNugget Number is any number that you can create by adding combinations of 4, 6, 9, and 20. For example, 49 is a McNugget number, since you can do 20 + 20 + 9 = 49. But poor 11 is not a McNugget number — there is no combination of adding numbers from the group {4, 6, 9, 20} that’ll get you to 11. Turns out, almost all numbers (well, integers) are McNugget numbers — in fact every positive integer over 11 can be produced using the McNugget number set. The McNugget club used to be a little more exclusive — back before the days of the 4-piece Happy Meal, you could find non-McNugget numbers all the way up to 43.
Hank Aaron famously broke Babe Ruth’s home run record when he hit his 715th home run back in 1974. As he rounded the bases on that momentous occasion, he almost certainly must have pondered the prime factors of 714 and 715:
714 factors into 2 x 3 x 7 x 17
715 factors into 5 x 11 x 13
If so, he must certainly have tried adding up the prime factors for each. It was probably as he was rounding third, as he added these prime factors in his head, that he must have made the delightful discovery: for both numbers, the prime factors add to 29 — the same number!
In honor of these two numbers, mathematicians have named this concept the Ruth-Aaron Pair — a Ruth-Aaron pair is a pair of consecutive numbers whose sum of prime factors are equal. All kidding aside, someone actually did describe this idea to Hank Aaron. Aaron nodded politely and co-signed a baseball with the great mathematician and number-theorist Paul Erdos, thereby giving Hank Aaron an Erdos number of 1.
Speaking of baseball, be careful if you’re ever hired to build and supply the bases for little league teams. In the Little League’s official rulebook, the specifications they give for the dimensions of home plate would require you to build a shape that can’t exist in our universe. Specifically, we’re talking about the front triangular-shaped tip of the plate. Someone decided to require the front triangular tip to be part of a right triangle (where the front tip is a right angle), but they didn’t check their work. Given the dimensions of the plate, it would have to be a 12 inch by 12 inch by 17 inch right triangle, which don’t satisfy the Pythagorean Theorem, and therefore cannot physically exist. Ponder that, little Billy, while you’re trying to get a hit in your next game!
The Well-Adjusted Integers
What does it take to make a number happy? As you might guess, it takes an arcane algorithmic procedure. A happy number is an integer that obeys a certain arbitrary-sounding property that I’m about to describe. Your reaction is going to be “what the hell? Why would anyone care about that?” Calm down, dammit – remember, this is number theory. Arcane arbitrary procedures are what we do every day. So here’s the procedure: take your favorite integer, and add together the squares of all of its digits. You now have a new number. Do it again — for this new number, take the sum of the squares of all the digits again. Keep going — like a mathematical Ouroboros, feed the answer back into this funny procedure. For some numbers, you’ll wind up converging on the number 1. These numbers are called happy numbers, and all other integers are called sad numbers. Poor saps. Instead of converging on 1, the sad numbers will wind up in an endless cycle looping through the same eight integers, but never reaching 1.
If you’re not a happy number, at least you can keep up appearances — a polite number is an integer that is the sum of two or more consecutive integers. For example, 13 is polite, since it happens to be 6 + 7. As for the nasty brutish integers that can’t be formed as the sum of consecutive integers, these are called impolite numbers. Some numbers can be “decomposed” like this in more than one way — the politeness of a number is the number of ways it can be expressed as the sum of consecutive integers. Turns out the number 90 has politeness equal to five, though I’m not going through the tedious process of checking that. (Is that impolite of me?)
Turns out the psychology of numbers is surprisingly rich. A perfect number is the sum of its divisors (other than itself) – for example, the divisors of 6 are 1, 2, and 3, and 1 + 2 + 3 = 6. They’re not very common – the next perfect number is 28, followed by 496 and 8128. Numbers can also be hyperperfect, almost perfect, weird, deficient, sociable, or amicable, or perhaps most ominously, untouchable. And this next one sounds like clear overcompensation to me: numbers can be absolutely normal. “Nothing to see here! I’m absolutely normal! There’s no bodies hidden in my trunk!”
This formula is tantalizingly close to being correct: if you computed both sides of the equation, they would agree all the way out to the 42nd decimal place:
The big ol’ mess on the left is only approximately equal to p/8, and it’s a coincidence – as far as we know there’s no good reason that they’re so close.
While we’re at it, here are a few more curious coincidences:
- Check this out – the value e ( p * sqrt(163)) is aaaallllmoooosttt an integer. It’s suuuuper close to 640320 3 + 744. They differ only in the 13th decimal place — so if you plugged it into a cheap calculator, it might claim that this value (called Ramanujan’s constant) is actually an integer. This leads into the wonderful world of almost integers — numbers that are for some reason veeeeryyyy close to an integer.
- 5882 + 23532 = 5882353
- The number of liters in a gallon is about 3 + p / 4, accurate to within one part in 500,000. (Thanks xkcd!)
Whoops! Pardon me! I didn’t mean to Emirp in mixed company. Don’t know what an Emirp is? Maybe you should elgoog it. An emirp is a prime number that, when you reverse its digits, is still a prime number. For example, the number 37 is prime, and when you flip the digits to get 73, you still have a prime. The largest known emirp is 1010006+941992101×104999+1, but I bet you could find a bigger one if you really tried (for once). A handful of primes are palindromic, meaning they’re the same number read forward or reverse. And I bet they’re just insufferable about it, too.
When I’m bored, I tend to doodle aimlessly, which is why the junk mail at my house tends to have pictures of people with mustaches (even women and children), teeth blackened out, monocles, top hats, and other accouterments not originally in the photo when it was taken. What do mathematicians doodle when they’re bored? Stan Ulam drew himself a spiral array of the integers while listening to a talk, and found himself pondering the shape’s unusual properties:
Boy, I always get the following constant stuck in my head:
Why? Well, because if you write this out in decimal form, you get:
J = 867.53090198…
If you read out the first seven digits, you’ll soon understand what I’m talking about – 867-5309 was the name of a gigantic one-hit-wonder from 1982 from the band Tommy Tutone. Those of you who know what I’m talking about are currently humming this inescapable ditty. Those of you who somehow missed this song, I assure you, someone did actually release a song named for a telephone number – and a real number at that, not one of those fake 555-… dealies. If you want your math to be a closer approximation to Top 40 radio, try the following:
And this is just the tip of the iceberg – spend some time exploring Wikipedia or MathWorld and you’ll come across all kinds of delightful topics. (For example, what the hell is Monstrous Moonshine?) If you have other topics you’d like to see written up (and snarked at) here, hit up Sean at TimeBlimp.com, or on twitter at @timeblimp.



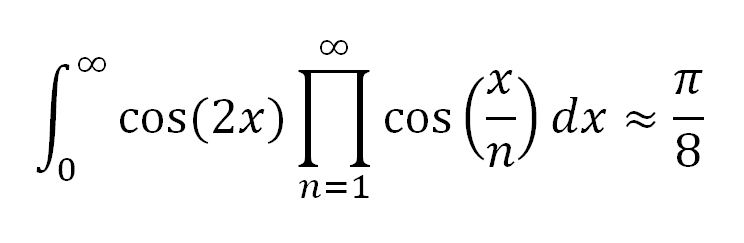



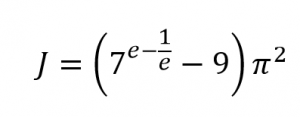
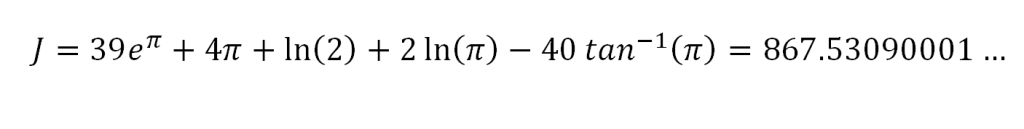

 Follow Timeblimp on Twitter
Follow Timeblimp on Twitter