Book Review: The Music of the Primes, by Marcus du Sautoy
 What a cool book! If you’re a fan of math, and not afraid of an equation or two, check out this very readable yet mathematically meaty historical account of a simple mathematical hypothesis. This book mostly focuses on number theory, more specifically on prime numbers, and even more super-specifically on the Riemann Hypothesis, probably the single most famous unsolved problem in math now that Fermat’s Last Theorem has been polished off. I’m a sucker for science / math books that actually bother to illuminate the personalities, the people behind the discoveries, as well as the math itself. Plenty of books can teach you about the Riemann Zeta function, but this one entertainingly dishes the dirt on the mathematicians themselves.
What a cool book! If you’re a fan of math, and not afraid of an equation or two, check out this very readable yet mathematically meaty historical account of a simple mathematical hypothesis. This book mostly focuses on number theory, more specifically on prime numbers, and even more super-specifically on the Riemann Hypothesis, probably the single most famous unsolved problem in math now that Fermat’s Last Theorem has been polished off. I’m a sucker for science / math books that actually bother to illuminate the personalities, the people behind the discoveries, as well as the math itself. Plenty of books can teach you about the Riemann Zeta function, but this one entertainingly dishes the dirt on the mathematicians themselves.
Names that might be familiar to math students from some theorem or technique are actually the names of real people – people like the frustratingly aloof Gauss, who likely discovered much more mathematics than we know about, but didn’t bother to write it down. The brilliant but painfully shy Bernhard Riemann (who formulated the mathematical hypothesis that is the star of this book), who in an extremely unfortunate personality impedance mismatch had the aloof Gauss as his mentor at the University of Gottingen (and barely spoke to him before Gauss died). The charming bohemian David Hilbert, who became the standard-bearer for math at the turn of the 20th century by laying out his famous 23 unsolved problems. Or Alte Selberg, the Norwegian mathematician whose preferred approach to mathematical collaboration (defiant solitude) was perhaps the complete opposite of Paul Erdos’ approach, with unfortunate consequences for both of them. And dozens more – stories illustrating the personalities behind the formulas, mostly awkward and shy geniuses, but a few bon vivants whom you’d like to have a beer with. Not to mention the city of Gottingen itself, which has been the backdrop of an astoundingly large amount of mathematical history (and later, of the development of Quantum Mechanics), which should be a prime destination for mathematically-minded tourists today. But let’s ignore them and get to the star of the book, the Riemann Hypothesis. How hard is it to comprehend a mathematical problem that has confounded the greatest geniuses of history, right up to this very day? Not too hard to sketch out in a blog post, in fact.
Take this not-too-complicated-looking equation – this bad boy is called the Riemann Zeta function:
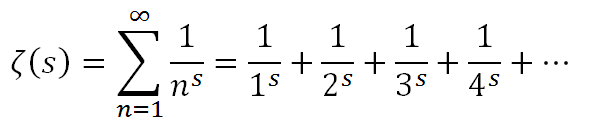 It’s pretty simple, for a math concept on the forefront of today’s research. You pick some number for the value for the variable “s”, add ‘em all up to infinity, and see what you get. If you plug in s = 1, you get this simple infinite series
It’s pretty simple, for a math concept on the forefront of today’s research. You pick some number for the value for the variable “s”, add ‘em all up to infinity, and see what you get. If you plug in s = 1, you get this simple infinite series
 This is what’s called the “Harmonic series”, and it turns out the answer is infinity – the sum just keeps getting bigger and bigger, without end. It’s probably not a major surprise that adding together an infinitely-long string of numbers winds up being infinite, huh? But it’s not true for all values of s – try s = 2, for example, and out pops a surprise:
This is what’s called the “Harmonic series”, and it turns out the answer is infinity – the sum just keeps getting bigger and bigger, without end. It’s probably not a major surprise that adding together an infinitely-long string of numbers winds up being infinite, huh? But it’s not true for all values of s – try s = 2, for example, and out pops a surprise:
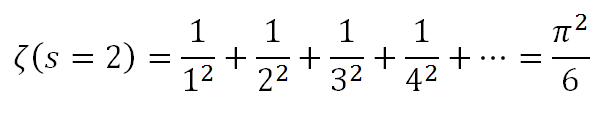 What??? It doesn’t equal infinity? An infinite number of terms, added up, actually sums to a finite value? And what the hell is Pi doing in there? If Pi’s cameo doesn’t seem a little mystically odd to you, then you might as well stop reading this article now. What could the proportions of a circle possibly have to do with that infinite sum up there? Even reading the proof, I still am amazed at this unexpected connection.
What??? It doesn’t equal infinity? An infinite number of terms, added up, actually sums to a finite value? And what the hell is Pi doing in there? If Pi’s cameo doesn’t seem a little mystically odd to you, then you might as well stop reading this article now. What could the proportions of a circle possibly have to do with that infinite sum up there? Even reading the proof, I still am amazed at this unexpected connection.
But hold onto your butt, because it’s about to get crazier – suppose we put in a complex number into the Riemann Zeta function. What happens then? Your ATM card is rejected, that’s what happens. Ha HA! Cough. Actually, nothing unusual happens – you can plug in a complex number just fine. For those who don’t remember their high school math, a “complex” number is sort of a compound number – it’s a “real” number plus an “imaginary” number, where a “real” number is just a plain old number that you’re familiar with, and an “imaginary” number is the square root of a negative number. Despite the name1, these are perfectly legitimate numbers in their own right, and eventually become ho-hum if you work with them for a while (say, in a college complex analysis class).
It turns out, if you plug in certain complex numbers for the variable s, add up the entire series, you get zero. That’s right, zero – the sum total of an infinite number of terms magically works out to exactly zero. And that’s pretty damn cool. Mathematicians are veeeerrrryyy interested about these values of s (which are called the “zeroes” of the function) where the infinite sum collapses to zero. In fact, understanding these zeroes is the key to the famous Riemann Hypothesis. Some of the zeroes are pretty simple, or “trivial”, in the dismissive jargon of mathematicians. It turns out that for s = -2, -4, -6, or any other negative even integer, the entire sum goes to zero. But if you want to hang with the cool kids, you need to check out the “non-trivial” zeroes – complex values for s (that have a real and an imaginary part) where the entire sum also goes to zero. These have earned the moniker “nontrivial”.
Check it out – here’s a plot of the Riemann Zeta function (thanks Wikipedia!), as you vary the imaginary part of s, with the real part of s kept fixed at ½ (for reasons I’ll explain in a moment). The spot where both the real part (red) and imaginary part (blue) both cross zero together is one of the famed Riemann Zeta zeroes. There’s one at about 14, another at about 21, and another at about 25.  So what do we want to know about them? For one thing, we’d like to know where they are. We know where many of them are (like the three in the plot above), but we’d like to know where all of them are. It turns out there are infinitely many zeroes out there, but we don’t yet have a way to derive them – you have to just stumble across them, more or less. So far, mathematicians have narrowed down a zone where zeroes are known to lurk – as it turns out, only complex numbers who have a real part greater than zero but less than 1 can be a zero (aside from some so-called “trivial” zeroes at the real numbers -2, -4, -6, …). What’s more, if you start checking particular zeroes, you’ll find them all to follow a compelling pattern – all of them that have been found so far have real part = ½. And we’ve found millions of them – every single one of them (so far) having a real-part equal to ½. The pattern was so suspicious that famous mathematician Bernhard Riemann hypothesized “hey, I think all of these zeroes are going to wind up with real part ½.” And that’s it – that’s the famous Riemann Hypothesis. So far it remains unproven, despite the fact that so far we’ve found ten trillion zeroes, and not a single damn one of them had a real part away from ½. Want to make a name for yourself in math? Prove that all zeroes must have real part = ½, and you’ll be rolling in mathematical fame for the rest of your life.
So what do we want to know about them? For one thing, we’d like to know where they are. We know where many of them are (like the three in the plot above), but we’d like to know where all of them are. It turns out there are infinitely many zeroes out there, but we don’t yet have a way to derive them – you have to just stumble across them, more or less. So far, mathematicians have narrowed down a zone where zeroes are known to lurk – as it turns out, only complex numbers who have a real part greater than zero but less than 1 can be a zero (aside from some so-called “trivial” zeroes at the real numbers -2, -4, -6, …). What’s more, if you start checking particular zeroes, you’ll find them all to follow a compelling pattern – all of them that have been found so far have real part = ½. And we’ve found millions of them – every single one of them (so far) having a real-part equal to ½. The pattern was so suspicious that famous mathematician Bernhard Riemann hypothesized “hey, I think all of these zeroes are going to wind up with real part ½.” And that’s it – that’s the famous Riemann Hypothesis. So far it remains unproven, despite the fact that so far we’ve found ten trillion zeroes, and not a single damn one of them had a real part away from ½. Want to make a name for yourself in math? Prove that all zeroes must have real part = ½, and you’ll be rolling in mathematical fame for the rest of your life.
Who cares? Why is this odd little result so compelling? It turns out the Riemann Zeta function has more unexpected connections besides a cameo from Pi – the location of the zeroes is intimately tied up with the location of prime numbers. And prime numbers are to mathematicians, what crack is to a certain former mayor of Toronto – an obsession often leading to disheveled appearances in public. Much like the location of the zeroes of the Riemann Zeta function, we don’t have a way to predict where prime numbers fall along the number line. We can easily test whether some integer is prime (for example, 17 is prime, but 21 is not), but what mathematicians would like to have is a formula – ideally, a formula that when you plug in the number N, returns the value of the Nth prime. So far all we’ve got are approximations to that formula. These approximations do decently well but don’t quite give you the right value for the Nth prime. It turns out that the location of the zeroes gets you an excellent approximate formula for the location of prime numbers, the best possible approximation, in fact. Gauss stumbled across a formula which is amazing now, and must have seemed like witchcraft at the time – the Nth prime number is approximately N * log(N). It’s not exact, but it does remarkably well, especially to help you count the number of primes at N or below. As it turns out, you can use the Riemann Hypothesis to develop a much more accurate (though still not perfect) formula – in fact, it has been proven that no other formula could possibly do better at predicting the location of primes.
The Riemann Hypothesis has turned out to be so useful in many branches of mathematics, that mathematicians often assume it’s true, and derive other theorems from there. Once someone slays the dragon, a whole army of other theorems will suddenly also be proven. In what has to be the strangest example of this, a proof of a theorem called Gauss’s Class Number Conjecture uses the Riemann Hypothesis whether it’s true or false – either way, the RH is used to prove the Conjecture. Du Sautoy brings us all the way to the present on the fascinating life of the Riemann Hypothesis and prime numbers, like the relationship to quantum mechanics (identified thanks to Freeman Dyson), the financial payoff of understanding prime numbers (via their use in encrypting sensitive information over the internet), or such interesting detours as mathematical modeling of the solitaire card game Klondike, or the fascinating world of Godel and his Incompleteness Proof (which did for math what Quantum Mechanics did to physics). Throughout du Sautoy juggles the focus between fascinating descriptions of the people with fairly in-depth descriptions of the math.
There are enough fascinating stories to keep me in Factwads for years. But let me give you perhaps my favorite – a formula discovered a little more recently, in 1976. Check out this monster:
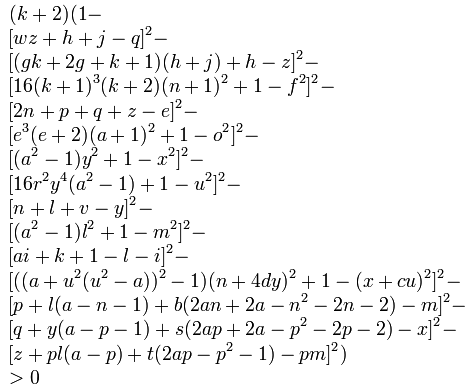 Despite how long it is, it’s a relatively simple formula – it’s just a polynomial, bigger than but in principle no different than the ones you dealt with back in algebra class. What makes this one so special? It happens to output prime numbers. If you pick random integers to plug in for all the variables a, b, c, … z, the resulting number will always be a prime number. You can generate every single prime number, with suitable choices for all 26 variables a through z. To me, that’s astounding. I gather from du Sautoy’s book that this is more of an interesting curiosity than a major breakthrough to modern mathematicians2, but still, I can’t even conceive of how you’d come up with this beast.
Despite how long it is, it’s a relatively simple formula – it’s just a polynomial, bigger than but in principle no different than the ones you dealt with back in algebra class. What makes this one so special? It happens to output prime numbers. If you pick random integers to plug in for all the variables a, b, c, … z, the resulting number will always be a prime number. You can generate every single prime number, with suitable choices for all 26 variables a through z. To me, that’s astounding. I gather from du Sautoy’s book that this is more of an interesting curiosity than a major breakthrough to modern mathematicians2, but still, I can’t even conceive of how you’d come up with this beast.
I see that once again, instead of reviewing a book, I’ve just given a series of tidbits about what’s in the book. But it’s a really fascinating book, a glimpse into a world where smart people prove concepts I can barely get my head around. I highly recommend it.
FOOTNOTES:
1. I hate these names, by the way – “imaginary” makes the concept of imaginary numbers seem so much more mysterious than it really is, and “irrational” is needlessly confusing.
2. In no small part due to a small caveat I didn’t mention – only when the formula outputs a positive number will that number be prime. Any time it outputs a negative number, the result is irrelevant to primes. And apparently this thing spits out mostly negative numbers, so it’s not a very practical tool for dealing with primes.

 Follow Timeblimp on Twitter
Follow Timeblimp on Twitter